BG_B1AR
About this model
This is a bond-graph model of beta-1 adrenergic receptor ( β-1AR) metabolism in the cardiac cell.
- INPUTS:
- Ligand (L) stimulus e.g. isoproterenol
- OUTPUTS:
- Change in molar amount of β-1AR (R),
- REACTIONS:
- Phosphorylation of β-1AR by β-ARK, producing β-1ARd
- Phosphorylation of β-1AR by PKACI, producing β-1ARp
Model status
The current CellML implementation runs in OpenCOR.
Model overview
This model is made by from an existing kinetic model, where the mathematics are translated into the bond-graph formalism. This describes the model in energetic terms and forces adherence to the laws of thermodynamics.
The creation of the composite LR and LRG species are not included in this module. See the module for L, R, and G binding for these.
For the following figures, all enzymes are shown in maroon.

Fig. 1. Original kinetic formulations.
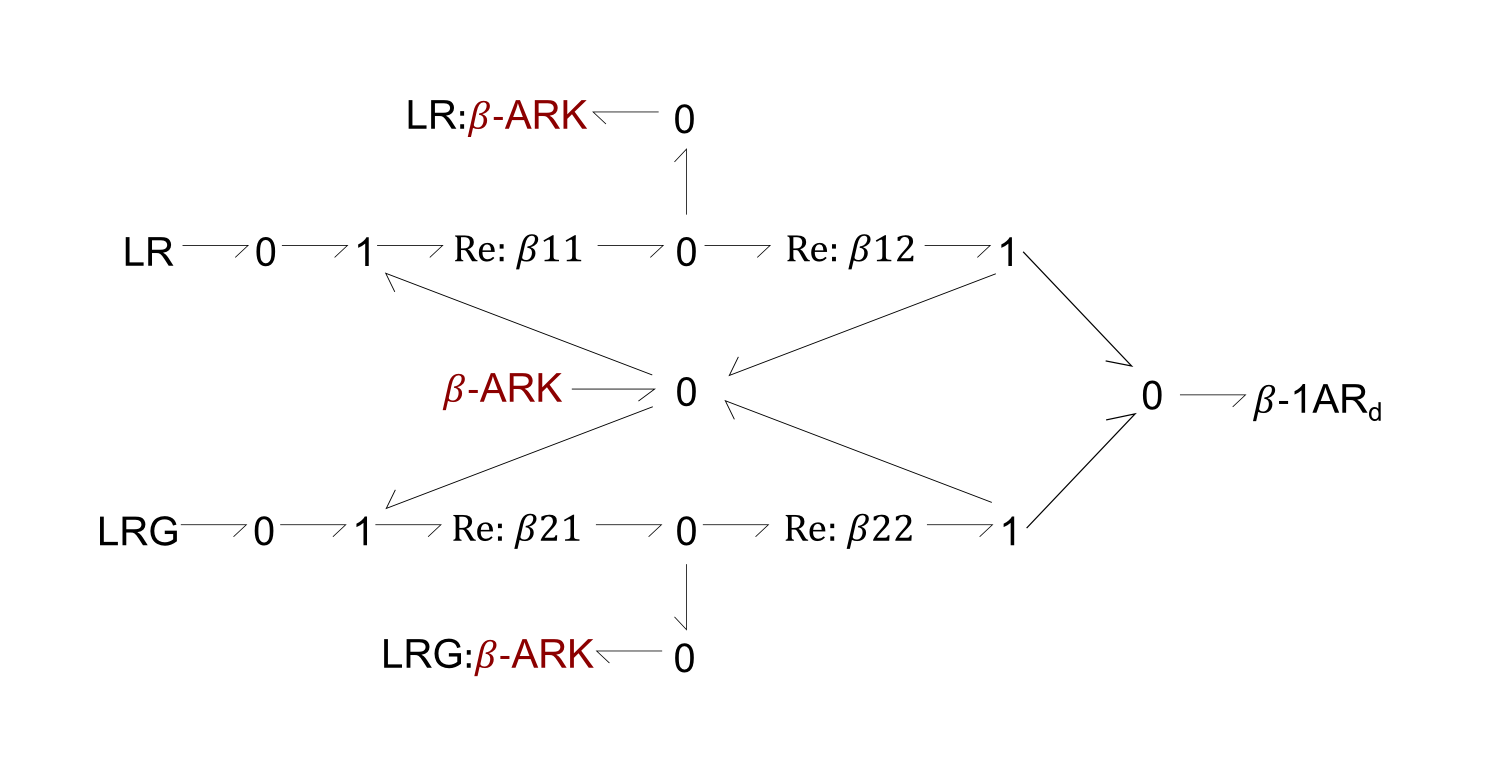
Fig. 2. Bond-graph formulation of the reaction involving the β-ARK enzyme, in the phosphorylation of β-1AR (Figure 1, left). The β-ARK enzyme was added as both a reactant and product to the original reaction, to show the fependence of the reaction rate on its concentration.

Fig. 3. Bond-graph formulation of the reaction involving the PKACI enzyme, in the phosphorylation of β-1AR at another site to the β-ARK enzyme (Figure 1, right).
For the above bond-graphs, a '0' node refers to a junction where all chemical potentials are the same. A '1' node refers to all fluxes being the same going in and out of the junction.
Parameter finding
A description of the process to find bond-graph parameters is shown in the folder parameter_finder, which relies on the:
- stoichiometry of system
- kinetic constants for forward/reverse reactions
- If not already, all reactions are made reversible by assigning a small value to the reverse direction.
Here, this solve process is performed in Python.
Original kinetic model
Saucerman et al: Modeling beta-adrenergic control of cardiac myocyte contractility in silico.
